This javascript application illustrates the proofs of Bell's theorem that arise from a set of measurements performed on five qubits. In summary, it allows a user to select sets of states only if they correspond to consistent (non-orthogonal) measurement results. The theorem is seen most directly from the fact that it is never possible to choose a state from every row, i.e. one for each of the seven measurements considered. 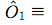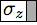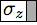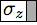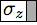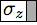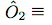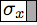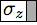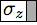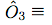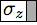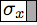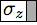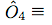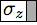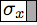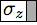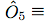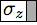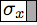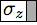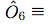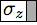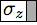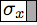By applying the results to distant measurements on entangled sets of qubits, we can conclude that a hidden variable theory can only succeed if it is nonlocally dependent on data from multiple spacelike-separated regions, in violation of the principle of causality.

[ Show / Hide ]         Overview

Summary of user control:  • Hover your cursor over any numbered state box (top-right table) to see its key properties including spin orientations, 32-D expansion and basis membership*. All measurements yield either (+1) or (-1). • Clicking on any state selects it and disables any others that are orthogonal to it, signifying that these disallowed states can never be observed to coexist with the current selection(s). The orthogonality conditions can be explored by making multiple selections and seeing how the remaining options become more constrained with every choice. Click on any disabled region to reset the selections. • The box symbolizing a particular basis is highlighted if one of its member-states has been selected. A red X is drawn over any whose members have all been prohibited by orthogonality, violating the completeness relation for that basis. These completeness conditions impose even greater constraints when imposed together with the orthogonalities. • Hoving over any basis box highlights the membership of that basis, furnishing its definition. Bell's theorem was the first of a series of no-go theorems ruling out local realism as an interpretation of quantum mechanics. It means that any attempt to describe QM as arising from a deeper classical (deterministic) theory would require superluminal influences, placing it in significant tension with relativity. The result is most well-known in the context of its original formulation, the Bell inequalities, expressing a limit on the statistical correlation between distant particles described by any local, deterministic theory. Over a wide class of experiments, these inequalities have been consistently violated and the quantum predictions have been consistently upheld. A lesser-known but arguably more important formulation is found in the Kochen-Specker theorem, or Bell-Kochen-Specker (BKS) theorem, which does not rely on inequalities but rather on sets of firm rules that are imposed by QM and are so far universally confirmed by experiment. Consequently, they reveal the result in a much more stark way. This program illustrates one such example of a BKS-type proof of Bell's theorem using five qubits. The basic building blocks of this BKS proof scheme are the six observables \(\hat{O}_1\) through \(\hat{O}_6\), defined as tensor products of Pauli spin operators (\(\sigma_x, \sigma_z\)) and 2-by-2 identity operators (\(\mathbb{I}\)). From these, and from the single-qubit Pauli operators themselves, we construct seven sets of commuting observables, or seven allowed ways to measure the system. These seven allowed measurements correspond to the seven rows of the top tables. The conspicuously missing last entry in the seventh row of the Observables Table plays a special role. This entangled basis corresponds to the simultaneous measurement of all six \(\hat{O}_i\), and thus the resulting eigenstates cannot be described in terms individual qubit spins but only in terms of their correlations, that is, of their \(\hat{O}_i\) eigenvalues. As will be shown in detail, it is a tension between this entangled basis and the other measurements that leads to the contradictions at the heart of the theorem. In the following sections I will first explain the most straightforward way of obtaining the BKS theorem: the observables proof. I will then describe the simple but vital logical step for turning these BKS theorem proofs into proofs of the much stronger Bell's theorem. It will also be shown that every observables proof is necessarily a restriction of a more extensive structure called a states proof. *For simplicity, I will sometimes use the word "state" to refer to any projector. In addition to rank-1 projectors, or normal states, this system also uses rank-4 projectors which specify the system to within a four-dimensional (two-bit) subspace. For the present purposes the word "state" is accurate enough. A similar remark applies to the "bases" that include these rank-4 projectors.

[ Show / Hide ]         Overview

[ Show / Hide ]         The Observables Proof

We first consider a single observer preparing to measure a system of five quantum bits. This observer chooses one of seven allowed (commuting) sets of simultaneous measurements. These seven sets of measurements correspond to the seven rows of the two tables at the top of the page. Six of these contain one of the multi-bit observables \(\hat{O}_i\) together with each of its constituent single-bit observables. The seventh is the simultaneous measurement of all the \(\hat{O}_i\). For definiteness I will call these seven choices of measurement sets \(M_1\) through \(M_7\) and list them below. $$ M_1 \equiv \{ \hat{O}_1 \ , \ \hat{\sigma}_{1z} \ , \ \hat{\sigma}_{2z} \ , \ \hat{\sigma}_{3z} \ , \ \hat{\sigma}_{4z} \ , \ \hat{\sigma}_{5z} \}$$ $$ M_2 \equiv \{ \hat{O}_2 \ , \ \hat{\sigma}_{1x} \ , \ \hat{\sigma}_{2z} \ , \ \hat{\sigma}_{5z} \}$$ $$ M_3 \equiv \{ \hat{O}_3 \ , \ \hat{\sigma}_{1z} \ , \ \hat{\sigma}_{2x} \ , \ \hat{\sigma}_{3z} \}$$ $$ M_4 \equiv \{ \hat{O}_4 \ , \ \hat{\sigma}_{2z} \ , \ \hat{\sigma}_{3x} \ , \ \hat{\sigma}_{4z} \}$$ $$ M_5 \equiv \{ \hat{O}_5 \ , \ \hat{\sigma}_{3z} \ , \ \hat{\sigma}_{4x} \ , \ \hat{\sigma}_{5z} \}$$ $$ M_6 \equiv \{ \hat{O}_6 \ , \ \hat{\sigma}_{1z} \ , \ \hat{\sigma}_{4z} \ , \ \hat{\sigma}_{5x} \}$$ $$ M_7 \equiv \{ \hat{O}_1 \ , \ \hat{O}_2 \ , \ \hat{O}_3 \ , \ \hat{O}_4 \ , \ \hat{O}_5 \ , \ \hat{O}_6 \}$$ Here we have adopted notation in which \(\hat{\sigma}_{jx}\) and \(\hat{\sigma}_{jz}\) refer to the standard Pauli operators \(\sigma_{x}\), \(\sigma_{x}\) acting in the \(j\)th qubit of the tensor product space, i.e. \(\hat{\sigma}_{2z}\equiv \mathbb{I}\otimes \sigma_z \otimes \mathbb{I}\otimes \mathbb{I}\otimes \mathbb{I} \). The astute reader may have already noticed the peculiarity in this construction that allows for the proof. Each of the measurement sets contains one extra bit of information that is fully dependent on the others, and thus does not add any additional knowledge. This one-bit redundancy reflects the fact that the product of all the operators in a set is proportional to the identity operator of the full Hilbert space. In the case of \(M_1\) through \(M_6\), the product is equal to \(\mathbb{I}\), and therefore the product of the resulting eigenvalues must be 1. In the case of \(M_7\), the product of the operators is \(-\mathbb{I}\) and therefore the product of the measured eigenvalues in this set must be -1. The importance of constructing the sets with this redundancy is that it describes an experiment which establishes the rules governing the relationships among these quantities unambiguously. The rules just described are guaranteed to hold with probability 100%, because the results with the wrong number of minus signs correspond to orthogonal subspaces, and so projecting onto them gives zero. To summarize, the rules are: Rule 1: When measuring one of the sets \(M_1\) through \(M_6\), we are certain to obtain an even number of -1 results. Rule 2: When measuring set \(M_7\), we are certain to obtain an odd number of -1 results. Quantum mechanics asserts that these rules are sure to hold, but only in the context of the allowed simultaneous measurements. It is senseless to talk about definite rules relating non-commuting operators because these quantities cannot be simultaneously determined, even in principle. Consistent with this, the rules just derived cannot accommodate even a single hypothetical assignment of predetermined values to all the quantities. So to prove the BKS theorem, we now assume that all observables can be predetermined prior to measurement, and then show that this leads to a contradiction. Rule 1 says that the value of any \(\hat{O}_i\) is equal to the product of the values for each of its constituent Pauli operators. This means that the product of all the \(\hat{O}_i\) values must be equal to the product of all the values occurring in the right side of the Observables Table. However, looking at the columns of the Observables Table, we see that each of the two single-qubit Pauli operators occurs twice in the definitions, therefore any minus signs must occur in pairs, and so the product of all the \(\hat{O}_i\) values must be +1. However, Rule 2 asserts that the product of the \(\hat{O}_i\) values must be -1 too, so we have arrived at the contradiction. If its initially confusing how this rather abstract argument connects to tangible physics, remember that it's exactly the role of this program to clarify the aspects of that connection. The double-occurence of the single-qubit Pauli spin operators in the definitions is obviously a critical element and the "Spin Correspondence Map" part of the program helps clarify what this means. Each of the sides of the pentagon in this figure symbolize one of the three-qubit observables (\(\hat{O}_2\) through \(\hat{O}_6\)). Each has two vertices that are shared with adjacent sides, symbolizing that sharing of two constituent \(\sigma_x\) operators. Similarly, the observable \(\hat{O}_1\) is composed of all \(\sigma_z\) operators, which lie in the center of the sides of the pentagon. Thus \(\hat{O}_1\) shares one constituent with each of the five other composite observables. The situation is summarized by the following guide: 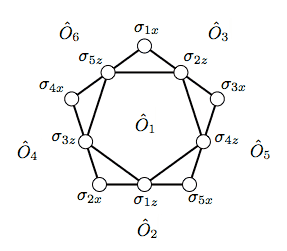If we suppose that a certain single-qubit Pauli observable has a particular value, then consistency requires that it have that same value no matter which set \(M_i\) it is measured in. For example, \(\sigma_{1x}\) may be measured in either \(M_3\) or \(M_6\). This gives rise to a network of consistency criteria among the outcomes of the various measurements. On its own, fixing an outcome for one \(M_i\) affects at least three others, reducing the total number of possibilities for each by one-half. We can see by using the program to specify various outcomes for the seven measurements that the number of remaining possibilities drops very rapidly due to the highly interrelated nature of the criteria. If we try to complete this process of selecting a result for each of the seven measurements, we will eventually end up with all the possibilities for some row ruled out. The observables proof shows that if the two rules given above are applied to all observables, then the product of all the \(\hat{O}_i\) values must be both +1 and -1. We can check that if our maximal selection of outcomes in the States Table terminates by eliminating the seventh row, then the measured values indicated in the Observables Table will correspond to a +1 product, violating Rule 2. On the other hand, if we create a maximal selection which includes a state from the seventh row, thereby eliminating one of the other rows, then we will see a -1 product in violation of Rule 1. Obviously, ruling out all the possible outcomes for one of the allowed measurements is itself an inconsistency. Formally, we say it is a violation of the completeness relation for the basis in question. These are the other major consistency criteria constraining the results of outcomes, and by extension, any potential hidden variable theories. They will play a more prominent roll in the generalization of this proof discussed later. First, we will show how this result can be extended to prove Bell's theorem.

[ Show / Hide ]         The Observables Proof

[ Show / Hide ]         From BKS to Bell's Theorem

In QM, the freedom to measure an observable simultaneously with any others that mutually commute doesn't have any effect on the statistics of the observables in question. For example the observable \(\sigma_{1z}\) occurs in both \(M_1\) and \(M_2\), and for any given initial state the probabilities of the possible outcomes are identical for either choice. In the context of attempts to devise a hidden variable theory, its not immediately obvious how to implement this principle. Even though there is no discernible effect on the statistics, we can not dismiss the possibility that the choice of measurement set effects the outcome in some way that does not manifest in the quantum statistics. There exists a possibility for a deterministic theory that is characterized not just by values for the observables, but also depends on the choice of commuting observables to measure. In the observables proof we assumed that this was not the case, and this assumption is called noncontextuality. It is a far weaker assumption than the nonlocal assumption of Bell's theorem, which rests on the inability to communicate faster than light. As we will now see, it is easy to rule out the contextual possibility and restore the full Bell's theorem based on the same set of observables. Like all proofs of Bell's theorem it is entanglement that allows this extension to take place. When two qubits are maximally entangled, the situation is generally summarized by saying they are either perfectly correlated or perfectly anti-correlated. A common example is of a source emitting two particles whose spins are perfectly anti-correlated due to conservation of angular momentum. For our purposes it is easiest and most pedagogically clear to use a perfectly correlated state, the so-called Bell state: $$ \left | B \right \rangle \equiv \frac{1}{\sqrt{2}}(\left| \uparrow \uparrow \right \rangle + \left| \downarrow \downarrow \right \rangle ) $$ This ensures that if Alice and Bob both measure their spins along the same axis, they are certain to get the same results. Notice that if we wish to apply a BKS theorem like ours to the more common anti-correlated state, \((\left| \uparrow \downarrow \right \rangle + \left| \downarrow \uparrow \right \rangle )/\sqrt{2}\), this can easily be recast in terms of the Bell state by simply defining Bob's \(x\) and \(z\) axes opposite to Alices. Now imagine that we've created five pairs of qubits in this state, and we send the first of each pair to one observer (Alice) and the second of each pair to another observer (Bob), and we further assume that the two are separated by some very large distance. We now consider an expanded version of the previous experiment in which both experimenters are free to choose one of the seven measurements to perform on their set of five qubits. The all-important point here is that the correlation between the observables of Alice and Bob holds even when they are measured within different sets of commuting observables. So this type of experiment allows explicit demonstration of the noncontextuality of the observables, or to be more precise, it demonstrates the local noncontextuality. Taking into account this new result, the only remaining options for explaining QM in terms of a deterministic hidden variable theory are those which are in some way nonlocal. In other words the outcomes of each measurement would have to depend on data at both distant locations. This is Bell's theorem. This rule for the results of the distant measurements provides an extra way to utilize and interpret this program: The possible ways to select two different entries from the States Table are exactly the results that are possible when the distant observers are measuring different sets of observables.

[ Show / Hide ]         From BKS to Bell's Theorem

[ Show / Hide ]         Generalization & The States Proof

As mentioned before, the orthogonality relations aren't the only important conditions that results of any measurements must satisfy. Each of the seven sets of observables defines a particular basis which is both orthonormal and complete, and thus each basis also imposes a completeness relation. Using these, we can rephrase the proof utilizing the most general type of quantum mechanical measurement; the positive operator-valued measure (POVM). This means asking the system a set of yes or no questions; "Are you in state __?". For any state \(\left | \psi \right \rangle \), this question corresponds to the projection operator formed as the outer product \(\left | \psi \right \rangle \left \langle \psi \right | \). It's easy to check that this is a hermitian operator with eigenvalues 0 and 1. For higher-rank projectors we can simply add together the projection operators for each dimension of the corresponding subspace. The states proof can be expressed by saying there is no way to assign a definite YES/NO result to each projector such that each basis contains exactly one YES. This follows immediately from the same logic as the observables proof. The fact that the bases are orthogonal immediately enforces both Rule 1 and Rule 2, manifesting here as the requirement that each POVM can yield at most one YES. In the observables proof we also assumed that every measurement produces an answer, which here is justified explicitly through the completeness conditions which constrain the POVM to at least one YES. To account for all the completeness relations, and also to make the states proof itself explicit, it is necessary to find all possible complete, orthogonal bases that can be formed from the eigenstates and eigenprojectors that are relevant for these measurements. This task that was the subject of original research done in pursuit of my undergraduate degree at WPI. A program was written to exhaustively find all the bases. There are 39 of them, and they're listed in the lower-right table of the program. The completeness requirement determines the way that projectors of various ranks can coexist in each basis, since the total dimensionality must agree with the dimensionality of the whole Hilbert space, which is 32. It turns out in this case that the bases come in three varieties, those with eight rank-4 projectors, those with four rank-4's and sixteen rank-1's, and those with 32 rank-1's or regular states. The definitions of any of these bases can be seen by hovering over the corresponding entry in the Basis Table. For the variation of this thought-experiment involving only two distant observers, the completeness relations do not affect which results are possible. However in analogous cases involving more than two observers they could come into play. Also, for anyone still wishing to formulate a nonlocal hidden variable theory, these relations provide additional constraints that must be contended with.

[ Show / Hide ]         Formal Mechanism